Pattern-based Rewrite Using Rules¶
Introduction¶
The ONNX Rewriter tool provides the user with the functionality to replace certain patterns in an ONNX graph with another pattern based on rewrite rules provided by the user.
Usage¶
There are three main components needed when rewriting patterns in the graph:
target_pattern: Original pattern to match against. This pattern is written as a function using ONNXScript-like operators.replacement_pattern: Pattern to replace the original pattern with. This pattern is also written as a function using ONNXScript-like operators.match_condition(optional) : Pattern rewrite will occur only if the match condition is satisfied.
A Simple Example¶
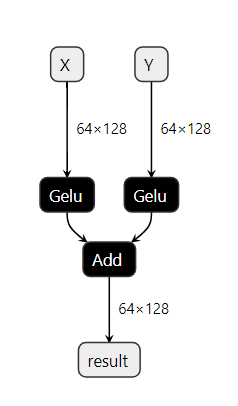
An simple example demonstrating the usage of this functionality using the GELU activation function:
GELU activation function can be computed using a Gauss Error Function using the given formula:
We will show how we can find a subgraph matching this computation and replace it by a call to the function.
Firstly, include all the rewriter relevant imports.
from onnxscript.rewriter import pattern
from onnxscript import ir
Then create a target pattern that needs to be replaced using onnxscript operators.
def erf_gelu_pattern(op, x):
return 0.5 * (x * (op.Erf(x / math.sqrt(2)) + 1.0))
After this, create a replacement pattern that consists of the GELU onnxscript operator.
def gelu(op, x: ir.Value):
return op.Gelu(x, _domain="com.microsoft")
Note
The inputs to the replacement pattern are of type ir.Value. For detailed usage of ir.Value refer to the ir.Value class.
For this example, we do not require a match_condition so that option is skipped for now. Then the rewrite rule is created using the RewriteRule function.
rule = pattern.RewriteRule(
erf_gelu_pattern, # Target Pattern
gelu, # Replacement Pattern
)
Now that the rewrite rule has been created, the next step is to apply these pattern-based rewrite rules. The rewriter.rewrite call consists of three main components:
model: The original model on which the pattern rewrite rules are to be applied. This is of typeonnx.ModelProto.function_rewrite_rules:(Optional)This parameter is used to pass rewrite rules based on function names. Steps on how to use this parameter will be covered in a different tutorial. This parameter is of typeSequence[type[FunctionRewriteRule]]pattern_rewrite_rules:(Optional)This parameter is used to pass rewrite rules based on a provided replacement pattern. For the purpose of this tutorial, we will be using only this parameter in conjunction withmodel. This parameter is of either one of these types:Sequence[PatternRewriteRule]RewriteRuleSet
Note
pattern_rewrite_rules takes a sequence of PatternRewriteRule types or a RewriteRuleSet which is also essentially a rule set created using a sequence of PatternRewriteRule types, so if only a singular rewrite rule is to be passed, it needs to passed as part of a sequence. For steps on how to create and use Rule-sets, refer to the example in the section Creating a rule-set with different patterns.
The snippet below below demonstrates how to use the rewriter.rewrite call for the rewrite rule created above:
def apply_rewrite(model):
rule = pattern.RewriteRule(
erf_gelu_pattern, # Target Pattern
gelu, # Replacement
)
model_with_rewrite_applied = onnxscript.rewriter.rewrite(
model,
pattern_rewrite_rules=[rule],
)
return model_with_rewrite_applied
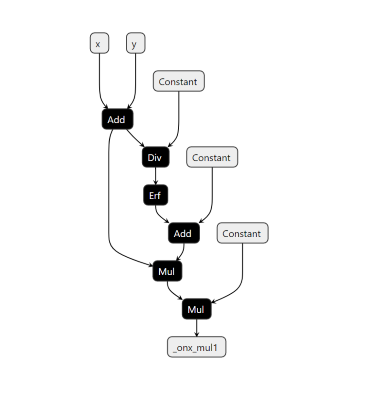
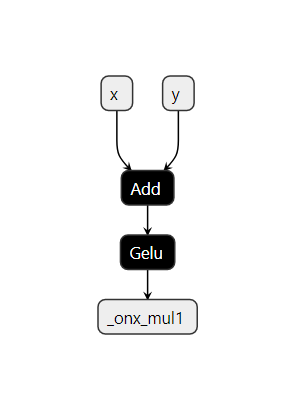
The graph (on the left) consists of the target pattern before the rewrite rule is applied. Once the rewrite rule is applied, the graph (on the right) shows that the target pattern has been successfully replaced by a GELU node as intended.
Specifying attributes in the pattern¶
This section demonstrates the use of attribute values in pattern-based rewriting.
First, write a target pattern and replacement pattern in a similar way to the previous examples.
The example pattern below will match successfully only against Dropout nodes with the
attribute value training_mode set to False.
The _allow_other_attributes option allows the pattern to match nodes that have additional attributes
not specified in the pattern. If it is set to False, then the node must have only the specified
attribute values, and no other attributes, for a successful match. The default value for this
option is True.
def add_pattern(op, input):
return op.Dropout(input, training_mode=False, _allow_other_attributes=True)
def add_replacement(op, input, **_):
return op.Identity(input)
def apply_rewrite(model):
# Create rewrite rules
add_rule = pattern.RewriteRule(
add_pattern, # target pattern
add_replacement, # replacement pattern
)
# Create a Rewrite Rule Set
rewrite_rule_set = pattern.RewriteRuleSet([add_rule])
# Apply rewrite while passing match_condition
model_with_rewrite = onnxscript.rewriter.rewrite(
model,
pattern_rewrite_rules=rewrite_rule_set,
)
return model_with_rewrite
Utilizing commute parameter for pattern-matching¶
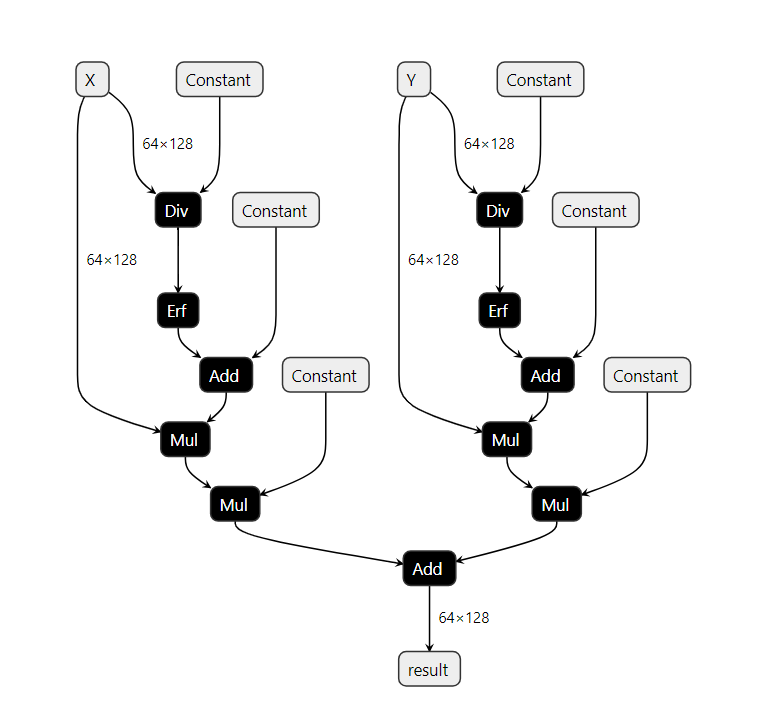
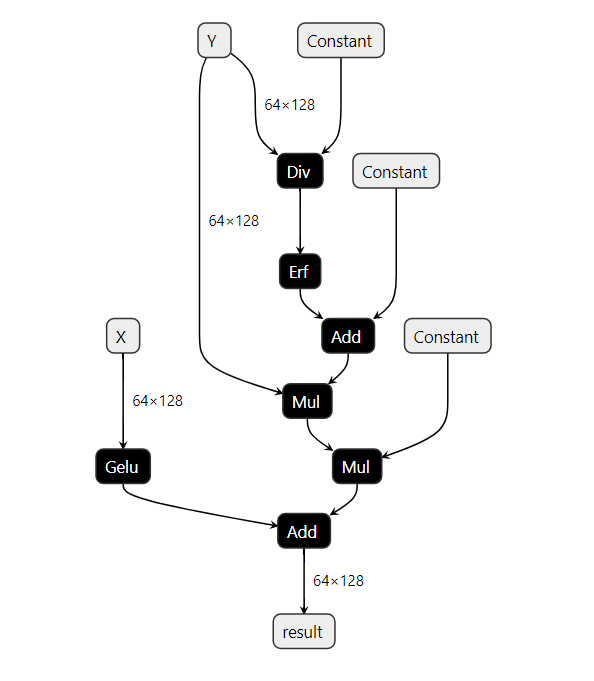
Extending the previous simple example, assumming a scenario where we have a graph with the following structure.
In this graph, there exist two node pattern that constitute a GELU op. However, there is a subtle difference between the two. Focusing on the parent Mul nodes in either patterns, the order of the input values being multiplied is switched.
If we utilize the same target_pattern created for the earlier simple example (shown below), only one of two GELU pattern will be matched.
def erf_gelu_pattern(op, x):
return 0.5 * (x * (op.Erf(x / math.sqrt(2)) + 1.0))
Only one of the patterns has been successfully matched and replaced by a GELU node. In order to rewrite both the existing patterns in the graph, there are two methods.
1. Creating a rule-set with different patterns.¶
This method requires creating two separate rules and packing them into either a sequence of PatternRewriteRules or a RewriteRuleSet. Creating a RewriteRuleSet is the preferable option but either can be used. In order to create a RewriteRuleSet with multiple rules rule1 and rule2 for example:
from onnxscript.rewriter import pattern
rewrite_rule_set = pattern.RewriteRuleSet(rules=[rule1, rule2])
In order to apply this method to the example above, first create the two separate target patterns as follows:
def erf_gelu_pattern(op, x):
return 0.5 * (x * (op.Erf(x / math.sqrt(2)) + 1.0))
def erf_gelu_pattern_2(op, x):
return (x * (op.Erf(x / math.sqrt(2)) + 1.0)) * 0.5
Then, create two separate PatternRewriteRules, one for each target pattern. Pack these rules into a RewriteRuleSet object and apply rewrites by passing the created RewriteRuleSet for the pattern_rewrite_rules parameter.
def apply_rewrite_with_ruleset(model):
# Create multiple rules
rule1 = pattern.RewriteRule(
erf_gelu_pattern, # Target Pattern
gelu, # Replacement
)
rule2 = pattern.RewriteRule(
erf_gelu_pattern_2, # Target Pattern
gelu, # Replacement
)
# Create a Rewrite Rule Set with multiple rules.
rewrite_rule_set = pattern.RewriteRuleSet([rule1, rule2])
# Apply rewrites
model_with_rewrite_applied = onnxscript.rewriter.rewrite(
model,
pattern_rewrite_rules=rewrite_rule_set,
# pattern_rewrite_rules=[rule1, rule2], # Alternative method of passing multiple rules
)
return model_with_rewrite_applied
2. Using the commute parameter while creating a rule.¶
Creating multiple target patterns for similar patterns can be tedious. In order to avoid this, the commute parameter can be utilized while creating the RewriteRuleSet. Simply set commute=True in order to avoid creating multiple target pattern for cases where patterns are different due to commutativity. Multiple rules with the different patterns emerging due to satisfying the commutativity property are automatically packed into a RewriteRuleSet object. Then apply rewrites by passing the created RewriteRuleSet for the pattern_rewrite_rules parameter.
def apply_rewrite_with_commute(model):
rule = pattern.RewriteRule(
erf_gelu_pattern, # Target Pattern
gelu, # Replacement
)
# Create a Rewrite Rule Set with commute=True
rewrite_rule_set = pattern.RewriteRuleSet([rule], commute=True)
# Apply rewrites
model_with_rewrite_applied = onnxscript.rewriter.rewrite(
model,
pattern_rewrite_rules=rewrite_rule_set,
)
return model_with_rewrite_applied
For the both of the aforementioned methods, the final graph with both rewrites applied should look as follows:
Using the match_condition parameter for pattern-matching¶
This section talks about how to utilize the match_condition parameter. The match_condition parameter checks if the pattern matches the target pattern with certain constraints in consideration.
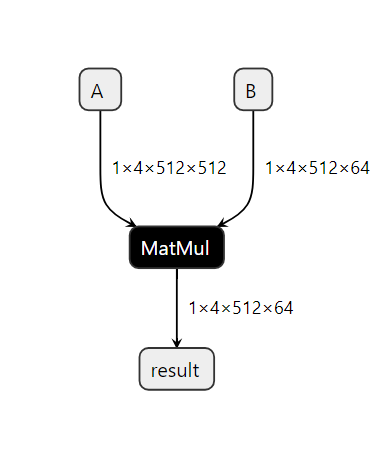
Let us consider a model which consists of the following pattern.
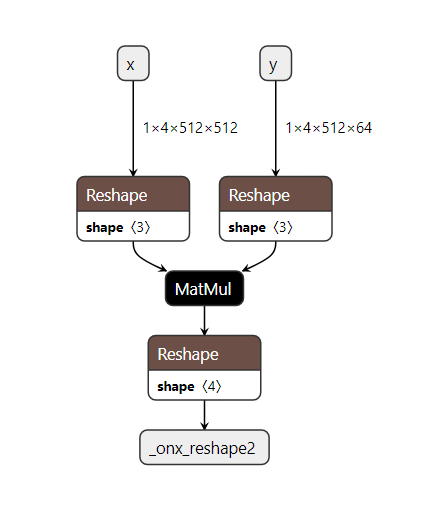
Based on the ONNX Matmul spec, onnx Matmul behaves like numpy.matmul and also follows numpy broadcasting. So in this particular pattern if matmul broadcasting is enough, then we don’t need the reshapes. To validate this, we need to check the following:
Input shapes check:
input_aandinput_bshould be broadcastableOutput shape check:
shape_cshould be the same as the output shape from thematmul(input_a, input_b)
If the above are true, then we don’t need the reshapes and we can eliminate them using a pattern based rewrite.
First, write a target pattern and replacement pattern in a similar way to the first example.
def two_reshapes_matmul_reshape_pattern(op, input_a, input_b, shape_a, shape_b, shape_c):
reshape_a = op.Reshape(input_a, shape_a)
reshape_b = op.Reshape(input_b, shape_b)
matmul = op.MatMul(reshape_a, reshape_b)
return op.Reshape(matmul, shape_c)
def matmul_pattern(op, input_a: ir.Value, input_b: ir.Value, **_):
return op.MatMul(input_a, input_b)
Note
The target pattern in this case has 5 inputs input_a, input_b, shape_a, shape_b, shape_c. However, the replacement pattern only utilizes input_a and input_b. To avoid referencing all the unused parameters in the replacement pattern signature, pass only input_a and input_b and use **_ to represent all the unused parameters.
Similarly for writing the condition checking function, we require only input_a, input_b and shape_c. Use **_ to represent all the unused parameters in the condition matching function signature.
In order to validate whether matmul broadcast is sufficient, we write a condition checking function as follows:
def check_if_not_need_reshape(
context, input_a: ir.Value, input_b: ir.Value, shape_c: ir.Value, **_
) -> bool:
"""Condition to check if we need to replace the pattern.
If matmul broadcasting is enough, then we don't need the reshapes.
To validate this, we need to check the following:
1. Input shapes check: input_a and input_b should be broadcastable
2. Output shape check: shape_c should be the same as the output shape from the matmul(input_a, input_b)
If the above are true, then we don't need the reshapes.
Returns:
True if we need to replace the pattern, False otherwise.
"""
del context # Reserved for future extensions
input_a_shape = input_a.shape
input_b_shape = input_b.shape
shape_c_tensor = shape_c.const_value
if shape_c_tensor is None:
logger.info("The value 'shape_c' is not statically known.")
return False
if len(shape_c_tensor.shape) != 1:
logger.info(
"Unexpected final shape. The shape of 'shape' value is %s",
shape_c_tensor.shape,
)
return False
# NOTE: When there is a subset match with a pattern. The MatchResult won't have the shape
# information. So, we need to check if the shape is None and return False.
if input_a_shape is None or input_b_shape is None:
logger.info("Shape information is not available for the inputs and outputs.")
return False
input_a_shape = input_a_shape.numpy()
input_b_shape = input_b_shape.numpy()
shape_c = shape_c_tensor.numpy().tolist()
a_rank = len(input_a_shape)
b_rank = len(input_b_shape)
# TODO(justinchuby): Check shape size
# 1. Check if input shapes are broadcastable
# 1.a. If the first input is 1-D, check whether
# the dim matches the last second dim of the second input.
mimic_matmul_broadcast_behavior = False
if a_rank < 2:
if b_rank < 2:
logger.info("Optimization of dot product is not supported yet.")
return False
if input_a_shape[-1] != input_b_shape[-2]:
logger.info("Original shape is not MatMul compatible.")
return False
else:
input_a_shape = [1, *input_a_shape]
a_rank = len(input_a_shape)
mimic_matmul_broadcast_behavior = True
# 1.b. If the second input is 1-D, check whether
# the dim matches the last dim of the first input.
if b_rank < 2:
if input_b_shape[-1] != input_a_shape[-1]:
logger.info("Original shape is not MatMul compatible.")
return False
else:
input_b_shape = [*input_b_shape, 1]
b_rank = len(input_b_shape)
mimic_matmul_broadcast_behavior = True
# 1.c. If both inputs are at least 2-D, check whether
# the last dimension of the first input matches the second
# last dimension of the second input, and shape[:-2] are
# broadcastable.
input_a_shape_except_second_last_dim = [*input_a_shape[:-2], *[input_a_shape[-1]]]
input_b_shape_except_last_dim = input_b_shape[:-1]
broadcast_matmul_output_shape = [input_a_shape[-2], input_b_shape[-1]]
for idx, (dim_from_a, dim_from_b) in enumerate(
zip(
reversed(input_a_shape_except_second_last_dim),
reversed(input_b_shape_except_last_dim),
)
):
if dim_from_a not in {1, dim_from_b}:
logger.info("Original shape is not broadcastable.")
return False
elif idx > 0:
broadcast_matmul_output_shape = [
max(dim_from_a, dim_from_b),
*broadcast_matmul_output_shape,
]
# 2. Check if output shape is the same as the output shape from the matmul(input_a, input_b)
# Prepend the broadcast_matmul_output_shape with the longer shape of input
if a_rank > b_rank:
longer_shape = input_a_shape
shorter_shape = input_b_shape
else:
longer_shape = input_b_shape
shorter_shape = input_a_shape
broadcast_matmul_output_shape = [
*longer_shape[: -len(shorter_shape)],
*broadcast_matmul_output_shape,
]
if mimic_matmul_broadcast_behavior and b_rank == 2 and input_b_shape[-1] == 1:
# If input_b is expanded to 2-D, then we need to remove the last dimension
broadcast_matmul_output_shape = broadcast_matmul_output_shape[:-1]
if mimic_matmul_broadcast_behavior and a_rank == 2 and input_a_shape[0] == 1:
# If input_a is expanded to 2-D, then we need to remove the first dimension
# of input_a, which would be the -2nd dimension of the output shape.
broadcast_matmul_output_shape.pop(-2)
if shape_c != broadcast_matmul_output_shape:
logger.info(
"Final output shape is not the same. Expected %s vs actual %s",
shape_c,
broadcast_matmul_output_shape,
)
return False
return True
With all the necessary components in place, the pattern rewrite rule with the match_condition function is created and then the rewriter.rewrite is called to apply the rewrite.
def apply_rewrite(model):
# Create rewrite rules
two_reshapes_matmul_reshape_rule = pattern.RewriteRule(
two_reshapes_matmul_reshape_pattern, # target pattern
matmul_pattern, # replacement pattern
check_if_not_need_reshape, # match_condition function
)
# Create a Rewrite Rule Set
rewrite_rule_set = pattern.RewriteRuleSet([two_reshapes_matmul_reshape_rule])
# Apply rewrite while passing match_condition
model_with_rewrite = onnxscript.rewriter.rewrite(
model,
pattern_rewrite_rules=rewrite_rule_set,
)
return model_with_rewrite
The final graph with the applied rewrite looks as follows: